
上面的人脸图片可以描述成多种不同属性,比如微笑、皮肤黑、男性、有胡须、不戴眼镜和头发黑等等。如果想要通过神经网络架构重构出这张人脸图片,可以先将图片编码成一个一个不同的属性,然后通过综合这些属性解码得到重构图片,这就是自动编码器的常规思路。
AutoEncoder和VAE
当潜在表示与原数据的关系复杂且非线性时,PCA将无法提取出最佳的潜在表示,这个时候我们用autoencoder来寻找更确切的潜在表示空间。
AutoEncoder
autoencoder是一种用神经网络来寻找某数据分布的非线性潜在表示的无监督学习方法,神经网络包括一个encoder网络(z=f(x))和一个decoder网络(\(\hat{x}=g(z)\))。
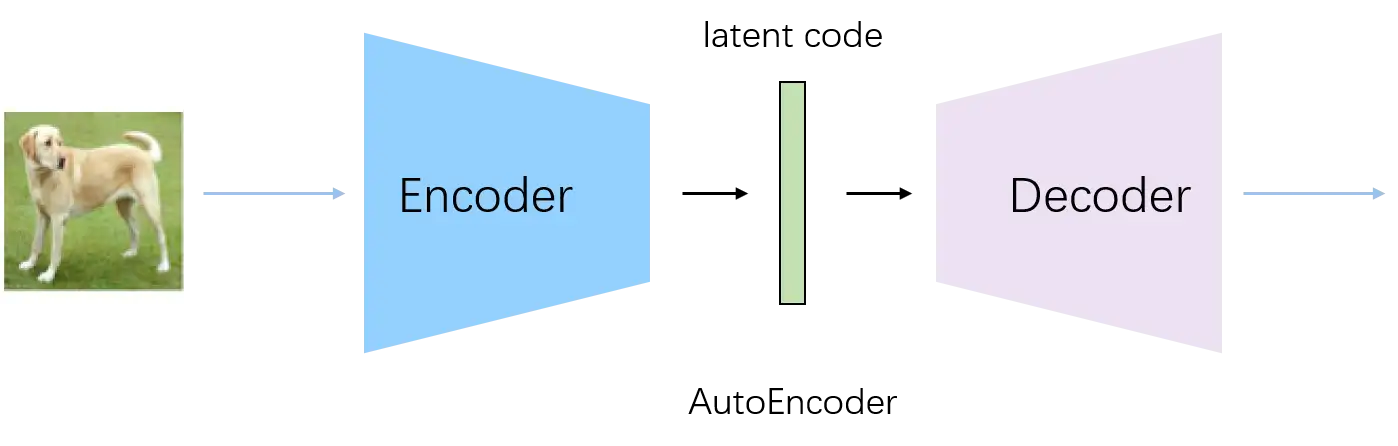
最基础的AutoEncoder由一个Encoder和一个Decoder组成。Encoder对输入图片进行编码得到latent code,然后通过Decoder进行重建,训练的时候最小化输入图片和生成图片的重构误差。
AutoEncoder可以理解为通过网络学习出任意概率分布,然后取概率分布中的最高点的横坐标作为编码的离散值。这会导致AutoEncoder的生成过程是不可控的,对输入噪声敏感,因为学习得到的概率分布是不能提前预知的。
VAE
autoencoder模型可以学习任一种潜在空间,这会导致学习到的数据点在潜在空间上杂乱纷离,其与VAE对比如下:

VAE通过在潜在空间上强制执行概率先验来克服这个问题。首先执行概率先验得到p(z),大多数情况下是一个标准高斯分布N(0,1)。对于一个数据点x,我们定义潜在空间的一个后验概率为p(z|x),我们的目标是计算该后验概率,使用贝叶斯公式\(p(z|x)=\frac{p(x|z)p(z)}{p(x)}\)。目前我们处理的是连续变量,p(x)难以计算,因此我们将后验概率近似值限制在一个特定的分布里即独立高斯分布,称为近似分布q(z|x),现在我们的目标是缩小真正后验和近似分布之间的KL散度,损失函数如下:
\[-E_{z-q(z|x)}[log(p(x|z))]+KL(q(z|x)||p(z))\]
其中q(z|x)由encoder近似,p(x|z)由decoder表示。第一项是重建损失,第二项是后验的规则化。后验被 KL 散度拉向先验,本质上将潜在空间正则化为高斯先验。 这具有保持潜在分布紧凑分布在 0 附近的效果。
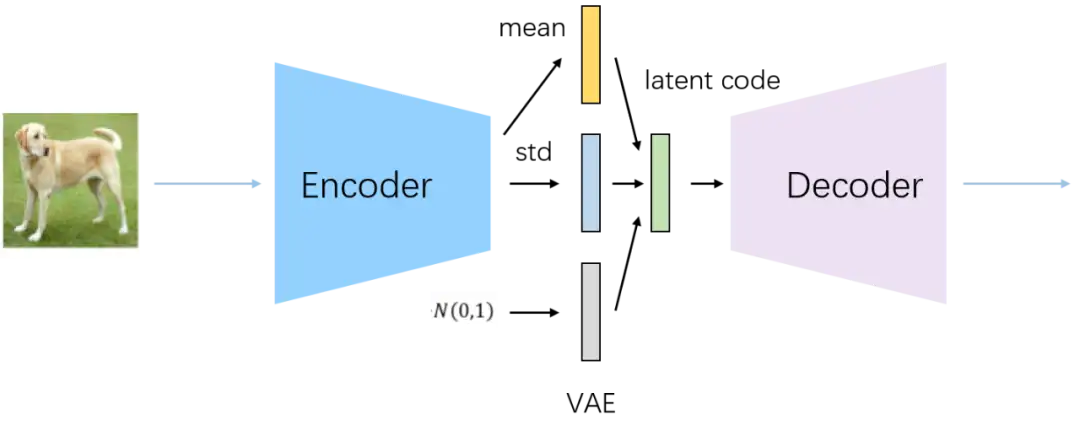
步骤如上图,通过Encoder学习出mean和std两个编码,同时随机采样一个正态分布的编码 ε ,然后通过 ε * std + mean公式重采样得到latent code,然后通过Decoder进行重建。另外,由于正态分布的连续性,不存在不可导问题,可以通过重参数方法,对latent code进行恢复,并且通过链式求导法则进行梯度更新。
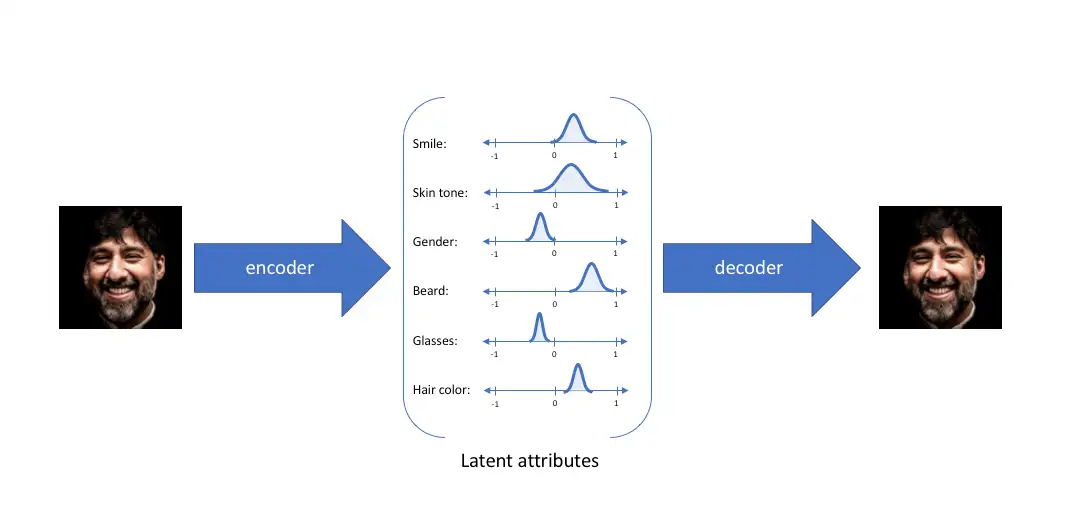
VAE可以理解为通过网络学习出每个属性正态分布的mean和std编码,然后通过mean和std和N(0,1)正态分布恢复每个属性的正态分布,最后随机采样得到每个属性的离散值。

如图所示,VAE相对于AutoEncoder的好处是,当采样输入不同时,VAE对于任意采样都能重构出鲁棒的图片。VAE的生成过程是可控的,对输入噪声不敏感,我们可以预先知道每个属性都是服从正态分布的,且各个属性之间的转变较为平滑。
VQVAE
VQVAE与VAE最大的不同就是,VQVAE学习的是一个离散的潜在表示。VQVAE在VAE上加了一个codebook,它是由相关索引向量构成的一个list,encoder输出与codebook中的所有向量进行比较,与其欧氏距离最近的向量会被输入到decoder中。
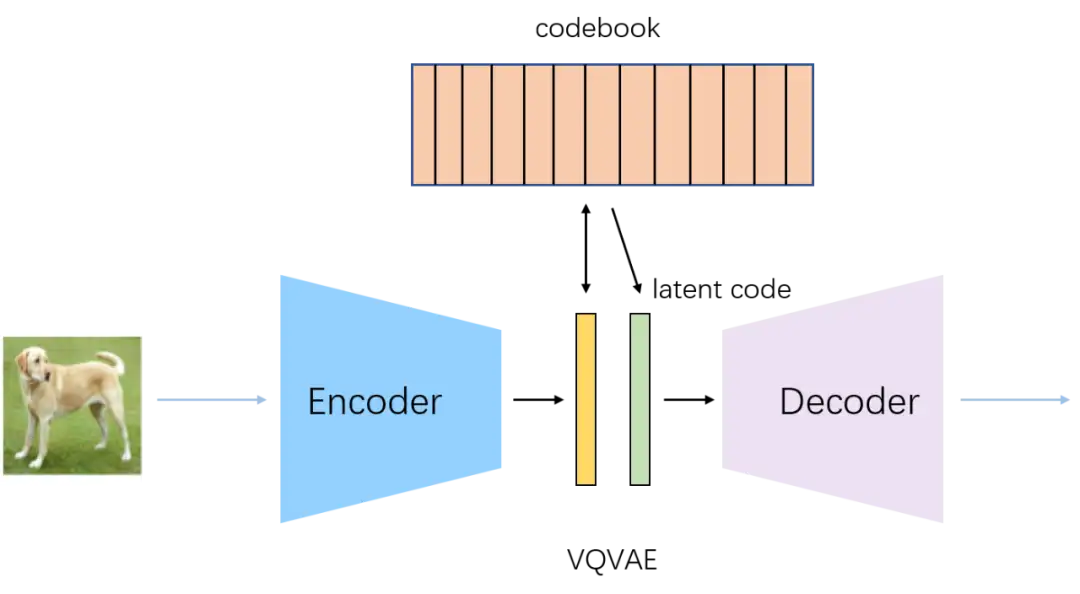
VQVAE通过Encoder学习出中间编码,通过最邻近搜索将中间编码映射为codebook中K个向量之一,然后通过Decoder对latent code进行重建。
另外由于最邻近搜索使用argmin来找codebook中的索引位置,导致不可导问题,VQVAE通过stop gradient操作,将decoder输入的梯度复制到encoder的输出上。
VQVAE相比于VAE最大的不同是,直接找每个属性的离散值,通过类似于查表的方式,计算codebook和中间编码的最近邻作为latent code。由于维护了一个codebook,编码范围更加可控,VQVAE相对于VAE,可以生成更大更高清的图片。
AutoEncoder、VAE和VQVAE可以统一为latent code的概率分布设计不一样,AutoEncoder通过网络学习得到任意概率分布,VAE设计为正态分布,VQVAE设计为codebook的离散分布。总之,AutoEncoder的重构思想就是用低纬度的latent code分布来表达高纬度的数据分布,VAE和VQVAE的重构思想是通过设计latent code的分布形式,进而控制图片生成的过程。
学习codebook
损失函数:\(log(p(x|q(x)))+||sg[z_e(x)]-e||^2+\beta||z_e(x)-sg[e]||^2\)
- 第一项:重建损失
- 第二项:codebook alignment loss,使选中的codebook向量尽可能接近encoder输出,sg是stop gradient,从而只更新codebook
- 第三项:codebook commitment loss,在codebook向量上使用stop gradient,使encoder输出尽可能接近codebook向量,权重由超参数\(\beta\)决定
最后两项是模型输出的每个量化向量的平均值。