概念
在多元统计分析中,主成分分析(英语:Principal components analysis,PCA)是一种统计分析、简化数据集的方法。它利用正交变换来对一系列可能相关的变量的观测值进行线性变换,从而投影为一系列线性不相关变量的值,这些不相关变量称为主成分(Principal Components)。具体地,主成分可以看做一个线性方程,其包含一系列线性系数来指示投影方向。PCA对原始数据的正则化。
基本思想
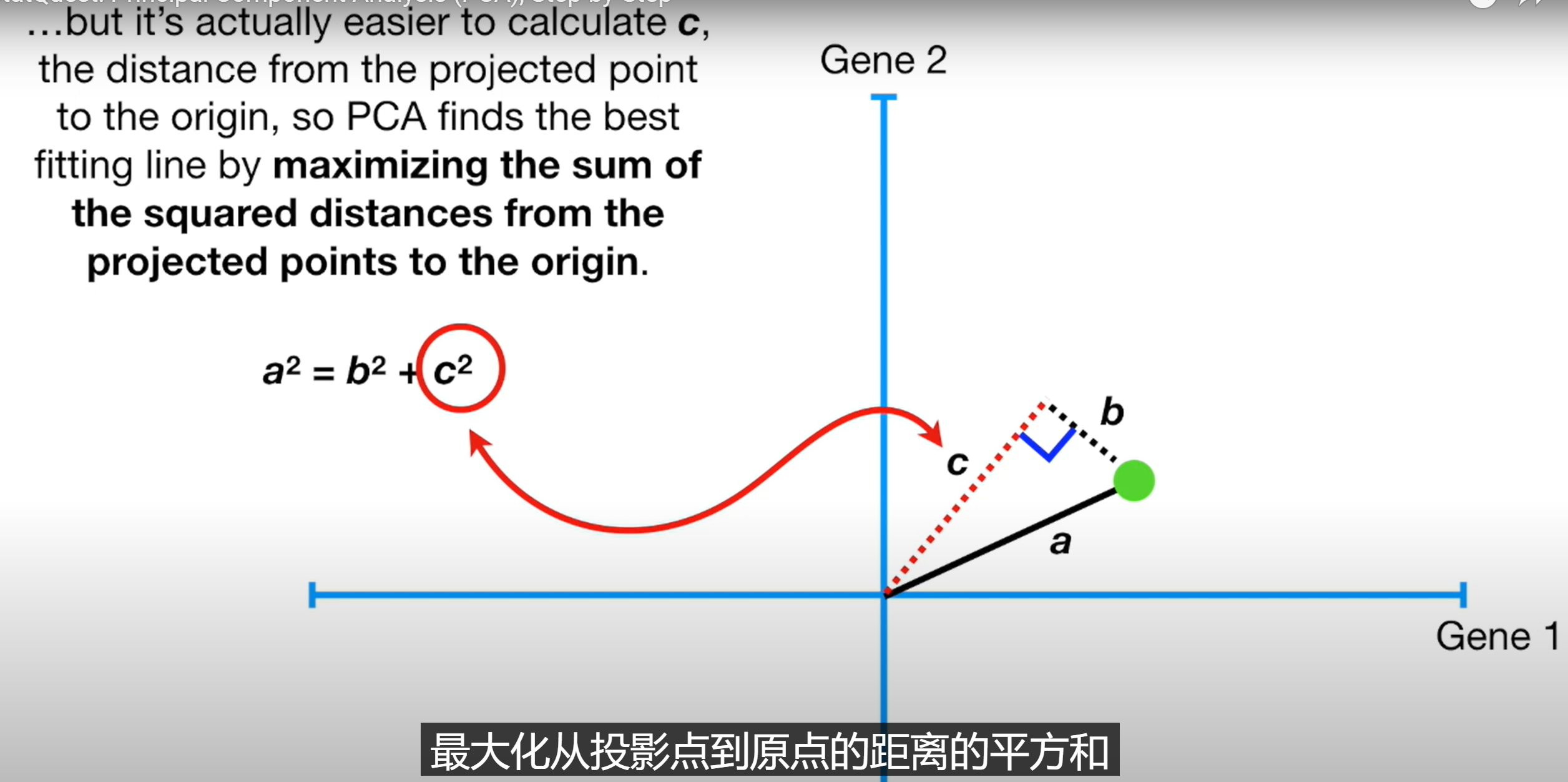
- 将坐标轴中心移到数据的中心,然后旋转坐标轴,使得数据在C1轴上的方差最大,即全部n个数据个体在该方向上的投影最为分散。意味着更多的信息被保留下来。C1成为第一主成分。
- C2第二主成分:找一个C2,使得C2与C1的协方差(相关系数)为0(C2轴与C1轴垂直),以免与C1信息重叠,并且使数据在该方向的方差尽量最大。
- 以此类推,找到第三主成分,第四主成分……第p个主成分。p个随机变量可以有p个主成分。
PCA将数据点到最佳拟合线的距离平方和(SS Distance)称为特征值,开根号后称为奇异值
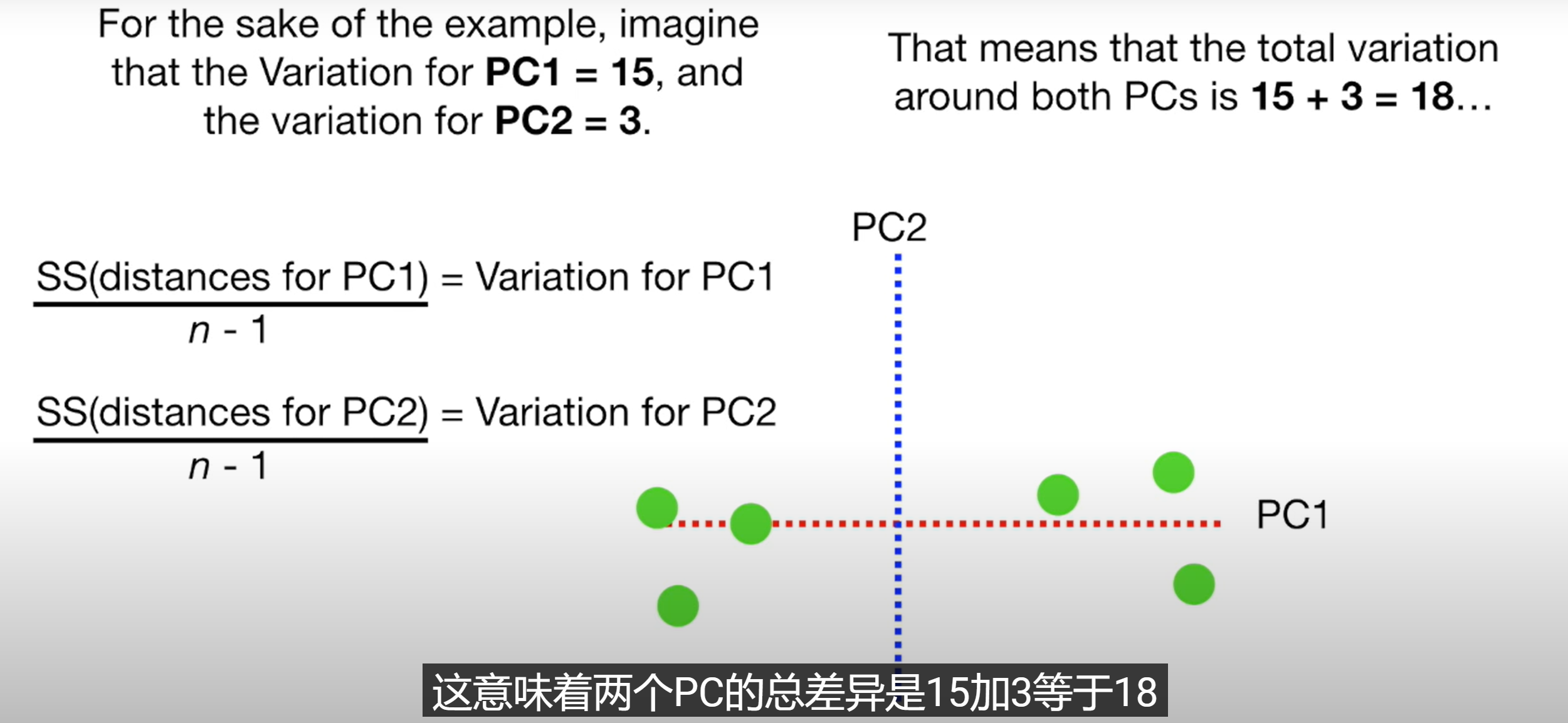
主成分分析经常用于减少数据集的维数,同时保留数据集当中对方差贡献最大的特征。这是通过保留低维主成分,忽略高维主成分做到的。这样低维成分往往能够保留住数据的最重要部分。但是,这也不是一定的,要视具体应用而定。由于主成分分析依赖所给数据,所以数据的准确性对分析结果影响很大。
特点
PCA是最简单的以特征量分析多元统计分布的方法。通常,这种运算可以被看作是揭露数据的内部结构,从而更好地展现数据的变异度。如果一个多元数据集是用高维数据空间之坐标系来表示的,那么PCA能提供一幅较低维度的图像,相当于数据集在讯息量最多之角度上的一个投影。这样就可以利用少量的主成分让数据的维度降低了。
PCA提供了一种降低维度的有效办法,本质上,它利用正交变换将围绕平均点的点集中尽可能多的变量投影到第一维中去,因此,降低维度必定是失去讯息最少的方法。PCA具有保持子空间拥有最大方差的最优正交变换的特性。然而,当与离散余弦变换相比时,它需要更大的计算需求代价。非线性降维技术相对于PCA来说则需要更高的计算要求。
PCA对变量的缩放很敏感。如果我们只有两个变量,而且它们具有相同的样本方差,并且成正相关,那么PCA将涉及两个变量的主成分的旋转。但是,如果把第一个变量的所有值都乘以100,那么第一主成分就几乎和这个变量一样,另一个变量只提供了很小的贡献,第二主成分也将和第二个原始变量几乎一致。这就意味着当不同的变量代表不同的单位(如温度和质量)时,PCA是一种比较武断的分析方法。
数学定义
PCA的数学定义是:一个正交化线性变换,把数据变换到一个新的坐标系统中,使得这一数据的任何投影的第一大方差在第一个坐标(称为第一主成分)上,第二大方差在第二个坐标(第二主成分)上,依次类推。
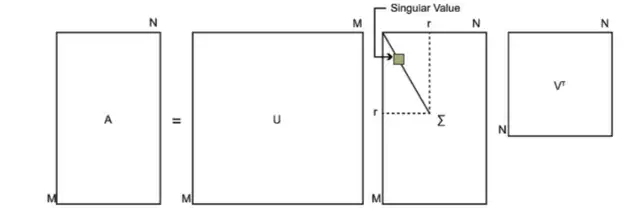
如果我们将A的转置和A做矩阵乘法,那么会得到n×n的一个方阵 \(A^TA\)。既然 \(A^TA\)是方阵,那么我们就可以进行特征分解,得到的特征值和特征向量满足下式:
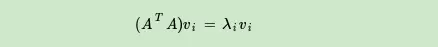
这样我们就可以得到矩阵 \(A^TA\)的n个特征值和对应的n个特征向量v了。将 \(A^TA\) 的所有特征向量张成一个n×n的矩阵V,就是我们奇异值分解(SVD)公式里面的V矩阵了。一般我们将V中的每个特征向量叫做A的右奇异向量。
如果我们将A和A的转置做矩阵乘法,那么会得到m×m的一个方阵\(AA^T\) 。既然\(AA^T\) 是方阵,那么我们就可以进行特征分解,得到的特征值和特征向量满足下式:
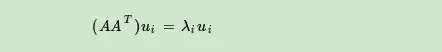
这样我们就可以得到矩阵\(AA^T\) 的m个特征值和对应的m个特征向量u了。将\(AA^T\) 的所有特征向量张成一个m×m的矩阵U,就是我们SVD公式里面的U矩阵了。一般我们将U中的每个特征向量叫做A的左奇异向量。
证明:
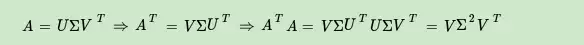
上式证明使用了 \(U^TU=I,Σ^T=Σ\)。可以看出 \(A^TA\)的特征向量组成的的确就是我们SVD中的V矩阵。类似的方法可以得到 \(AA^T\)的特征向量组成的就是我们SVD中的U矩阵。
可以看出特征值和奇异值满足如下关系:

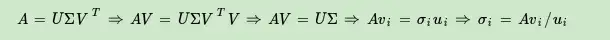
我们可以用 \(σ_i=Av_i/u_i\)来计算奇异值,也可以通过求出 \(A^TA\)的特征值取平方根来求奇异值。
PCA降维,需要找到样本协方差矩阵 \(X^TX\) 的最大的d个特征向量,然后用这最大的d个特征向量张成的矩阵来做低维投影降维。可以看出,在这个过程中需要先求出协方差矩阵 \(X^TX\),当样本数多样本特征数也多的时候,这个计算量是很大的。注意到我们的SVD也可以得到协方差矩阵\(X^TX\)最大的d个特征向量张成的矩阵,但是SVD有个好处,有一些SVD的实现算法可以不求先求出协方差矩阵 \(X^TX\) ,也能求出我们的右奇异矩阵V。也就是说,我们的PCA算法可以不用做特征分解,而是做SVD来完成。这个方法在样本量很大的时候很有效。实际上,scikit-learn的PCA算法的背后真正的实现就是用的SVD,而不是我们我们认为的暴力特征分解。
假设我们的样本是m×n的矩阵X,如果我们通过SVD找到了矩阵\(XX^T\)最大的d个特征向量张成的m×d维矩阵U,则我们如果进行如下处理: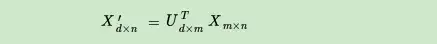
可以得到一个d×n的矩阵X’,这个矩阵和我们原来的m×n维样本矩阵X相比,行数从m减到了d,可见对行数进行了压缩。
左奇异矩阵可以用于行数的压缩。
右奇异矩阵可以用于列数即特征维度的压缩,也就是我们的PCA降维。
用统计方法计算PCA
组织数据集
假设有一组M个变量的观察数据,我们的目的是减少数据,使得能够用L个向量来描述每个观察值,L < M。进一步假设,该数据被整理成一组具有N个向量的数据集,其中每个向量都代表M个变量的单一观察数据。
- \(x_1…x_N\)为列向量,其中每个列向量有M 行。
- 将列向量放入M × N的单矩阵X里。
计算经验均值
- 对每一维m = 1, …, M计算经验均值
- 将计算得到的均值放入一个M × 1维的经验均值向量u中
计算平均偏差
- 从数据矩阵X的每一列中减去经验均值向量 u
- 将平均减去过的数据存储在M × N矩阵B中:B=X-uh,h是一个长度为N的全为1的行向量
求协方差矩阵
- 从矩阵B中找到M × M的经验协方差矩阵C
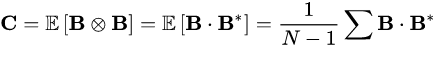
计算协方差矩阵的特征值和特征向量
- 计算矩阵C的特征向量
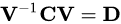
其中,D是C的特征值对角矩阵