CNN
CNN实质是通过中心像素点以及相邻像素点的加权和来构成feature map,实现空间特征提取,加权系数就是卷积核的权重系数。

那么卷积核的系数如何确定的呢?是随机化初值,然后根据误差函数通过反向传播梯度下降进行迭代优化。卷积核的参数通过优化求出才能实现特征提取的作用,GCN的理论很大一部分工作就是为了引入可以优化的卷积参数。
CNN处理的图像或者视频数据中像素点(pixel)是排列成成很整齐的矩阵,即Euclidean Structure,对于Non Euclidean Structure,也就是图论中的拓扑图,其每个顶点的相邻顶点数目都可能不同,CNN无法用一个同样尺寸的卷积核来进行卷积运算,因此无法处理。
主要思想
GCN是一种能够直接作用于图并且利用其结构信息的卷积神经网络。
对于每个结点,我们都要考虑其所有邻居以及其自身所包含的特征信息。假设我们使用average()函数,那对每一个结点进行上述操作后,就可以得到能够输入到神经网络的平均值表示。

每一个结点代表一篇文章,而边代表代表引用情况。在这里首先有一个预处理的步骤,也就是将论文的原始文本通过NLP嵌入的方法先转化为向量。接下来我们考虑绿色结点。首先得到包括其自身的所有节点的特征值,然后取平均,然后该平均值向量可以输入到一个神经网络中,再得到一个向量。
实际应用当中我们可以采用更为复杂的聚合函数,GCN神经网络的结构也可以比上面图中的网络结构更复杂。如下图就是一个两层全连接GCN的例子,每一层的输出都作为下一层的输入。

拉普拉斯矩阵
Graph Fourier Transformation及Graph Convolution的定义都用到图的拉普拉斯矩阵,计算方法如下

常用的拉普拉斯矩阵有三种:
- Combinatorial Laplacian:\(L=D-A\)
- Symmetric normalized Laplacian:\(L^{sys}=D^{-1/2}LD^{-1/2}\)
- Random walk normalized Laplacian:\(L^{rw}=D^{-1}L\)
在高维的欧氏空间中,一阶导数就推广到梯度,二阶导数就是拉普拉斯算子。
推导
考虑graph上的热传播模型,研究任一结点 i ,它的温度随着时间的变化可以用下式来刻画:
\(\frac{d\phi_i}{dt}=-k\sum_iA_{ij}(\phi_i-\phi_j)\)
A是邻接矩阵。继续推导:

右边括号里面的第二项,这可以认为是邻接矩阵的第 i 行对所有顶点的温度组成的向量做了个内积。
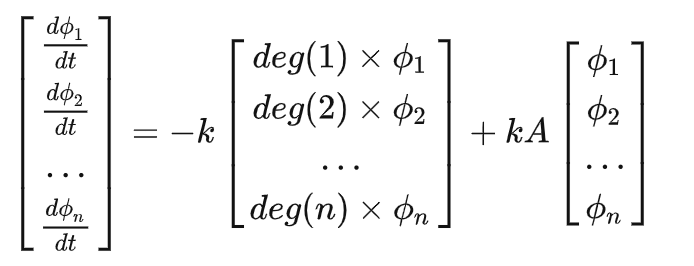
然后我们定义向量\(ϕ=[ϕ1,ϕ2,…,ϕn]^T\),就有:
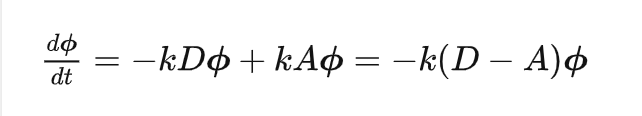
其中 D=diag(deg(1),deg(2),…,deg(n))被称为度矩阵,只有对角线上有值,且这个值表示对应的顶点度的大小。整理整理,我们得到:
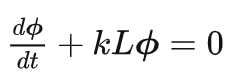
推广到GCN
GCN就是在一张Graph Network中特征(Feature)和消息(Message)中的流动和传播!这个传播最原始的形态就是状态的变化正比于相应空间(这里是Graph空间)拉普拉斯算子作用在当前的状态。
建模方面就衍生出了各种不同的算法,不一定要遵从牛顿冷却定律,可以引入核函数、引入神经网络等方法把模型建得更非线性更能刻画复杂关系。
解决方面,因为很多问题在频域解决更加好算,可以通过Fourier变换把空域问题转化为频域问题,解完了再变换回来。
原理

要如何才能够得到一个结点的邻居的特征向量的信息呢?一个可能的解决方法就是将A与X进行相乘。

这样做的缺点是:1.遗漏了结点本身的信息 2.应该使用平均值函数甚至是更好的加权平均值函数而非直接加和来处理邻居的特征向量。使用加和函数的时候,具有较大度值的结点会有很大的表示向量,而较低度的结点会有较小的聚合向量,这可能会导致梯度爆炸或梯度消失的问题(比如使用sigmoid函数时)此外,神经网络对于输入数据的标度是非常敏感的,我们需要将这些向量进行标准化以消除潜在的问题。
我们可以通过在A的基础上加上一个单位阵得到新的邻接矩阵\(\tilde{A}\),
\[\tilde{A}=A+\lambda I_N \tag{1}\]
当λ的取值为1时,意味着结点本身特征的重要性与其邻居的重要性一样。

对\(\tilde{D}^{-1}\)与X进行相乘,可以得到包括结点自身以及其邻居的特征向量的均值。

在直接使用 \(\tilde{D}^{-1}(\tilde{A}X)\)进行计算的时候有一个问题,就是\(\tilde{A}\)是对称的,我们只对其行进行了标准化而并没有对列进行标准化。

因此尝试使用\(\tilde{D}^{-1}\tilde{A}\tilde{D}^{-1}X\)进行标准化。

这种标准化的策略所提供的是一种加权平均,所实现的效果是会给予那些具有低度的结点更大的权重从而降低高度结点的影响。如上图,要得到结点B的聚合特征时,会分配较大的权重给B(其自身,度为3),而给E(度为5)更小的权重。
为进一步优化标准化的策略,避免上述方法中的两次标准化,可以采用\(\tilde{D}^{-1/2}\tilde{A}\tilde{D}^{-1/2}X\)进行标准化。


2-layer GCN:

GCN网络层数
网络的层数代表着结点特征所能到达的最远距离。比如一层的GCN,每个结点只能得到其一阶邻居身上的信息。对于所有结点来说,信息获取的过程是独立、同时开展的。当我们在一层GCN上再堆一层时,就可以重复收集邻居信息的过程,并且收集到的邻居信息中已经包含了这些邻居结点在上一个阶段所收集的他们的邻居结点的信息。这就是GCN的网络层数也就是每个结点的信息所能达到的maximum number of hops。因此,我们所设定的层的数目取决于我们想要使得结点的信息在网络中传递多远的距离。需要注意的是,通常我们不会需要结点的信息传播太远。经过6~7个hops,基本上就可以使结点的信息传播到整个网络,这也使得聚合不那么有意义。

由图可知,2~3层的网络应该是比较好的。当GCN达到7层时,效果已经变得较差,但是通过加上residual connections between hidden layers可以使效果变好。
总结
- GCNs可以用于网络中的半监督学习问题
- GCNs可以用于学习网络中结点的特征与网络结构的信息
- GCN的主要思想是对每个结点的邻居及其自身的信息作加权平均,从而得到一个可以传入神经网络的结果向量。
- 可以通过加深GCNs以获得更大的信息传播范围,如果要较大的层数,需要残差连接以提升效果。通常使用2~3层的GCN。
- 当图看作矩阵时,可以当作是一种矩阵标准化的过程。