概念
用数组来模拟树形结构,可以解决大部分基于区间上的更新以及求和问题
原理
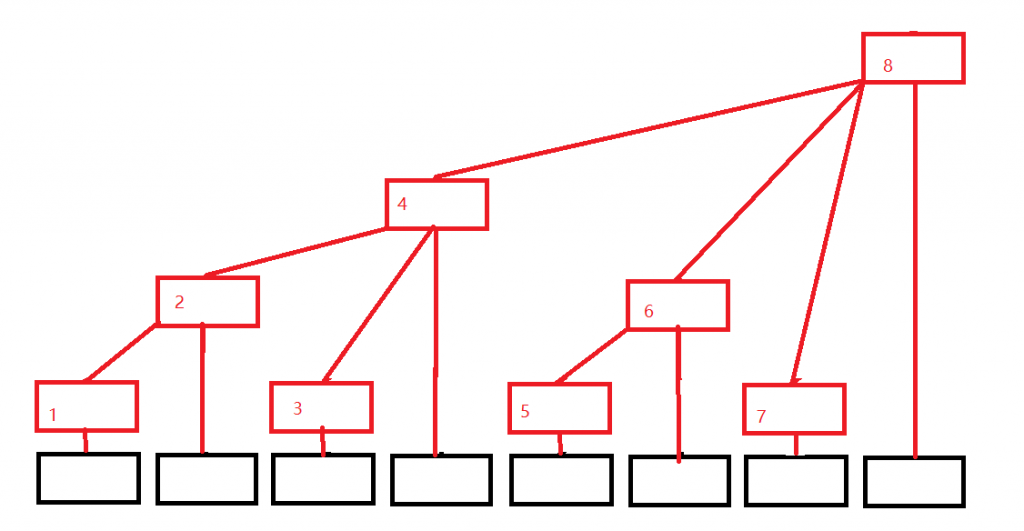
黑色:原数组A[]。红色:树状数组C[]
$$
C[i]=A[i-2^k+1]+A[i-2^k+2]+…+A[i]
$$
$$
k=lowbit(i)=i\&(-i)
$$
当i为0时结果为0;当i为奇数时结果为1;当i为偶数时结果为i中2的最大次方因子。
建立树状数组
若更新A[i],会影响到所有包含A[i]的位置。A[i]包含于C[i+lowbit(i)]、C[i+lowbit(i)+lowbit(i+lowbit(i))]…
单点更新,单点查询
传统数组
单点更新,区间查询
int n; //原数组的长度
int a[1005],c[1005]; //对应原数组和树状数组
int lowbit(int x){
return x&(-x);
}
void update(int i,int k){ //在i位置加上k
while(i <= n){ //给受影响的C[i]都加上k
c[i] += k;
i += lowbit(i);
}
}
int getsum(int i){ //求A[1 ~ i]的和
int res = 0;
while(i > 0){
res += c[i];
i -= lowbit(i); //对应树结构中C[i]左上的节点
}
return res;
}
int main(){
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i];
update(i,a[i]) //输入初值相当于更新值
}
cin>>x>>y;
int sum=getsum(y)-getsum(x-1); //x-y区间和
update(x,y); //A[x]加上y
update(x,-y); //A[x]减去y
}
区间更新,单点查询
利用差分建树:
$$
D[j]=A[j]-A[j-1] \\ A[i]=\sum^i_{j=1}D[j]
$$
例如A[]=1 2 3 5 6 9,D[]= 1 1 1 2 1 3
若将A[2~5]区间都加上2,则A[]=1 4 5 7 8 9,D[]= 1 3 1 2 1 1
区间内的值改变了,但是区间的差值是不变的,只有D[2]和D[6]改变
因此利用D[]来构建C[]
int n; //原数组的长度
int a[1005],c[1005]; //对应原数组和树状数组
int lowbit(int x){
return x&(-x);
}
void update(int i,int k){ //在i位置加上k
while(i <= n){ //给受影响的C[i]都加上k
c[i] += k;
i += lowbit(i);
}
}
int getsum(int i){ //求D[1 ~ i]的和,即A[i]
int res = 0;
while(i > 0){
res += c[i];
i -= lowbit(i); //对应树结构中C[i]左上的节点
}
return res;
}
int main(){
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i];
update(i,a[i]-a[i-1]); //利用差分构建C[i]
}
//A[x~y]区间内都加上k
update(x,k); //A[x]-A[x-1]增加k
update(y+1,-k); //A[y+1]-A[y]减少k
//查询A[i]
cin>>i;
int ai=getsum(i);
return 0;
}
区间更新,区间查询
由上可知
$$
\begin{align} \sum^n_{i=1}A[i]&=\sum^n_{i=1}\sum^i_{j=1}D[j]\\ &=D[1]+(D[1]+D[2])+…+(D[1]+D[2]+…+D[n])\\ &=n*D[1]+(n-1)*D[2]+…+D[n]\\ &=n*(D[1]+D[2]+…+D(n))-(0*D[1]+1*D[2]+…(n-1)*D[n])\\ &=n*\sum^n_{i=1}D[i]-\sum^n_{i=1}((i-1)*D[i]) \end{align}
$$
令sum1[i]=D[i],sum2[i]=D[i]*(i-1),分别维护这两个数组对应的树状数组C1[]、C2[]
int n;
int a[1005];
int c1[1005],c2[1005];
int lowbit(int x){
return x&(-x);
}
void update(int i,int k){
int add=k*(i-1); //D[i]增加k后,sum2[i]的增量
while(i<=n){
c1[i]+=k;
c2[i]+=add;
i+=lowbit(i);
}
}
int getsum(int i){ //求前缀和
int res=0,n=i;
while(i>0){
res+=n*c1[i]-c2[i];
i-=lowbit(i);
}
return res;
}
/*
更好理解的getsum:
int getsum(int i){ //求前缀和
int res=0,n=i,sum1,sum2;
while(i>0){
sum1+=c1[i];
sum2+=c2[i];
i-=lowbit(i);
}
res=n*sum1-sum2;
return res;
}
*/
int main(){
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i];
update(i,a[i]-a[i-1]);
}
//A[x,y]区间加上k
update(x,k); //A[x]-A[x-1]增加k
update(y+1,-k); //A[y+1]-A[y]减少k
//求A[x~y]的区间和
int sum=getsum(y)-getsum(x-1);
return 0;
}
优缺点
优点:修改和查询复杂度都是O(logN),相比线段树系数要少很多,比传统数组快,容易写
缺点:不能解决复杂的区间问题
查询任一区间和可以将大区间分成O(logN)数量的小区间,故复杂度为O(logN)